Chapter 2 Dimensions
“I always said if I had one breakfast to eat before I die, it would be Wonder Bread toasted, with Skippy Super Chunky melted on it, slices of overripe banana and fresh crisp bacon.”
Former NYC mayor Michael Bloomberg is a chunky peanut butter kind of person. Are you? As peanut butter comes in “smooth” and “chunky” varieties (also known as creamy and crunchy, respectively), this question is also a dichotomous one. However, if we add this test question to our question pool, in addition to the one about toilet paper orientation, we will soon find that having two two-kinds-of-people questions begins to imply more than two kinds of people. Wait, what?
See, back when I went to talk to the people in Washington Square, I also asked them about the great peanut butter debate. As you can see from Table 2.1, smooth came out slightly ahead.
| counts | |
|---|---|
| chunky | 17 |
| smooth | 23 |
But this second question did not erase the first question about toilet paper. In fact the first few rows of our data from Washington Square are displayed below. Each row, representing one person, now has two columns, labeled “roll” (for toilet paper) and “spread” (for peanut butter):
## roll spread
## 1 under chunky
## 2 over chunky
## 3 under smooth
## 4 over chunky
## 5 under smooth
## 6 under chunkyYou may have noticed that among the first six people for whom I have shown data, none of them answered both over and smooth. But such response pairs exist. In fact, if we count each combination as it occurs–that is, under-chunky, over-chunky, under-smooth, and over-smooth–we get the results shown in Table 2.2. There are four combinations, because we have two questions with two possibilities (dichotomies) for each.
Before you read on, it’s a good time to ask yourself if you can answer the following questions (answers in the footnote): (a) if there were two questions with three categories each, how many combinations could be observed? (b) if there were three dichotmous questions, how many combinations could be observed?4
| chunky | smooth | |
|---|---|---|
| over | 10 | 13 |
| under | 7 | 10 |
Table 2.2 is an example of a kind of table that is so common in data science, it has its own name. Three of them, in fact. It is sometimes called a cross table (or crosstab), or a two-way table (makes sense), but most commonly it is known as a contingency table (wha? I’ll explain later) I’m sorry that there are three names for the same thing. Really I am.
If you’re like me, you can’t resist paying some attention to the values in the Table 2.2. For example, you might notice that one of the cells of the table (over AND smooth) has the highest number of people in it. We can say that this is the modal category, referring to the mode, which is the most common value in a distribution of values. We have four possible values in this example.
Ok, now things are about to get deep. This first module is “How Many Kinds of People are There?” And we’ve now explored how using two two-kinds questions leads to four types. You’ve probably figured out yourself that you have to multiply the number of categories in each of the questions, and that tells you how many “buckets” you can have overall. But still, there are different ways to arrive at a certain number of buckets.
| counts | |
|---|---|
| chunky | 13 |
| don’t care | 3 |
| hate all | 4 |
| smooth | 20 |
Consider Table 2.3 in contrast to 2.2. We’ve now given people four choices to express their peanut butter preference. In addition to chunky and smooth, they can also choose to say that they hate all peanut butter or don’t care. We now have four kinds of people. But since we make the determination of what kind of person you are using just one question, we say that there is one dimension (in this case, peanut butter preference) along which people can be divided into four groups. In Table 2.2, there were two dimensions, a dimension of peanut butter and a dimension of toilet paper. Notice that this word, dimension, is used in much the same way as when we refer to geometric space as being two-dimensional (e.g., a drawing on flat sheet) or three-dimensional (e.g., a solid object, or sometimes a drawing that creates the illusion of looking at a solid object.) The three dimensions of space are often labeled something like (x, y, z). Here, our two dimensions could be labeled (pb, tp). The order doesn’t matter. We are merely indicating that there are two different variables used in categorizing our data (people, in this case). To summarize, in Table 2.2, we have two dimensions and four kinds. In Table 2.3, we have one dimension and four kinds.
So far so good: two questions, two dimensions, right? Well… maybe. We already saw that if a question does not actually divide people into kinds, because only one answer appears, then it doesn’t really count. It is not a dimension, because it is not really a variable. It does not vary; it is constant. In our contingency table representation, this might look like the left side of Table 2.4. In an alternate universe, no one prefers smooth to chunky. Another way to say it is that the peanut butter question is not informative because it has no variance. Everyone in our sample is the same.
|
|
But now consider the alternate universe on the right of Table 2.4. In that case, everyone who is an over-hanger of toilet paper prefers smooth peanut butter, and everyone who is an under-hanger prefers chunky. If this is the case, there are only two kinds of people, at least in our sample. Those who over-hang and prefer smooth and those who under-hang and prefer chunky. But does it make sense to say there are two dimensions? We did ask two different questions!
You might reason about it the following way: in our sample, if I ask anyone just one of the two questions–about either toilet paper or peanut butter–then I immediately know the answer they would give to the other one. Another way to say this is that the answer to one question completely determines the answer to the other, and thus the relationship between these questions (really, the answers) is deterministic. I don’t actually have to ask two questions, other than to establish in the first place that I didn’t have to. And since I only get information from one question, there is only one dimension.
Independence, Association, and Contingency
This section title sounds like a philosophy book by the late Richard Rorty. — inner voice
We just spent a little bit of time in an alternate universe, a bizarro world in which knowing how someone prefers to orient their toilet paper tells you what style of peanut butter they like, and vice versa. Notice that this knowing-about relationship is symmetric, and that in fact, the two representations as shown in Table 2.5 are informationally equivalent.
|
|
In our regular universe, however, this relationship was not observed. In Table 2.2, all four possible combinations occur. When knowledge about a person’s answer to one question provides information about their answer to another question, we say that the two answers are contingent upon one another. This is the reason we called the two-way table a contingency table in the first place, although it is still called that even when two answers are not contingent. Go figure. Contingent is another word for dependent. To make matters worse, we also often say that the two responses are associated.
In our bizarro world scenario, one answer completely determines the other. This deterministic relationship is one extreme in the spectrum of association/dependence/contingency. It expresses a certainty in knowing the answer to one question if we know the answer to another. At the other extreme, if the two responses are not at all associated/dependent/contingent, then we say that they are independent. To say that two responses are independent is to assert that knowing one of them does not give you any information about what the other one might be. This would have been my intuition, at least, about toilet paper and peanut butter. Somewhere in the middle, we might say that one answer gives you some information, but not certainty about another answer. Whether two answers are independent or mildly associated with one another is an empirical question, which means we should try to answer it with data. In bizarro world, where they were deterministically related, we might reasonably want to know why. Could there be a gene that controls both toilet paper orientation and peanut butter preference at the same time?
Latent Factors and Measurement
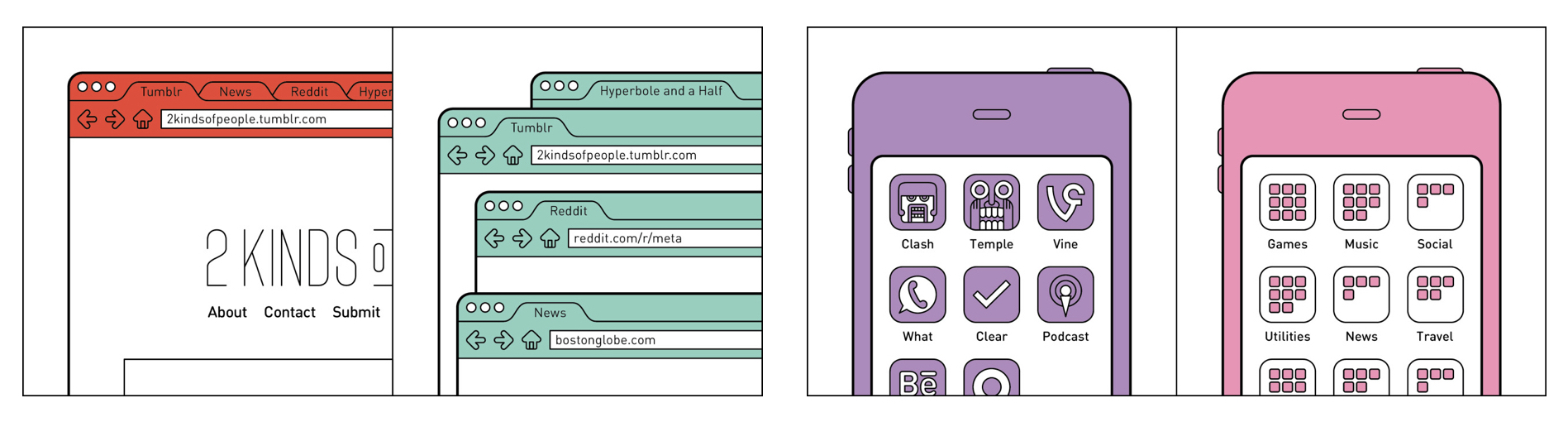
Figure 2.1: Two more two-kinds questions
Figure 2.1 (source) shows two more two-kinds of people graphics from João Rocha’s blog. I bet that you can identify yourself with one of the two images in each pair. I certainly can. But ask yourself, given our discussion above, do you think the choices a person would identify in each case above are independent or not independent (e.g., contingent, associated, dependent)?
In contrast to the toilet paper and peanut butter questions, which at least appear to be about totally different things, these two dichotomies have something similar going on in each of them. The choice on the left is about organizing your desktop browser, either in tabs or as separate windows. The choice on the right is about organizing apps in your smartphone, either loose or in folders. We might say that both of them get at a tendency to organize your digital environment. Call it digitidness (short for digital tidiness). This tendency, we may imagine, might even carry over into non-digital environments, like your actual desk, bookshelf, or filing cabinet.
What we’ve done here is to try to explain the association between responses to the two questions (assuming that there is, i.e. that they are not independent) by appeal to some underlying latent factor. We say a factor is latent (meaning hidden) because we don’t observe digitidiness itself directly, but we only observe tidy browsers or smartphone app folders. Perhaps you can think of another candidate factor besides digitidiness. In any case, we might propose that both of the two two-kinds questions in Figure 2.1 are in effect indirect measurements of the same factor. If so, this could explain why the two answers would be associated.
Notice that a factor is also a dimension, in the sense we used before. We could have said “latent dimension”, but we tend to use the word factor when we are drawing attention to the specific nature of the dimension rather than just counting. We also sometimes use the word trait. At least in psychology, trait tends to be reserved for stable psychological factors. Thus “stress” can be a factor but not a trait, whereas “social anxiety” may be a trait, if it is persistent. In this case, digitidiness might be considered a trait (and thus also a factor and a dimension).
Contrast this with toilet roll orientation, which we can observe directly just by looking in someone’s bathroom. (We assume that they are telling the truth when they answered our questions, but we could in principle verify it.) It was only in the bizarro world when toilet roll orientation and peanut butter preference were perfectly related that we started to wonder if there maybe was an underlying genetic factor. Genetic factors were once not directly observable either, but we assumed them for explanatory value. Today we can of course observe specific genetic variation, although there are still many gaps in our understanding of the relationship between genes and observed behaviors.
Consider some data again, in two possible worlds, shown in Table 2.6. On the left, we have the deterministic scenario we saw before. As before, we identified this situation as having two kinds of people and really just one dimension. In contrast to before, where we had no real explanation for this coincidence, we attribute it now to some factor, like digital tidiness.
|
|
But now consider the possible results in the table on the right. Since all four possible quadrants have non-zero counts, we see that knowing whether someone organizes their browser using tabs does not completely (i.e., deterministically) specify whether or not they put their apps into folders. On the other hand, one answer does seem to be associated with the other. Notice that the values are still much higher in the diagonal “buckets” that we think of as indicating the presence or absence of digitial tidiness. These are the tabs-folders bucket (tidy) or the windows-loose bucket (not tidy). We say that the tidiness factor appears to explain much of the observed range, or variance, in responses to the two questions. But it doesn’t explain all of it, since there are people (11 out of 40, in this case) who don’t fall into one of these buckets.
This situation on the right is probably more realistic. After all, very few things in this world are absolute (unlike in bizarro world). So now the big question re-emerges: are there two kinds of people or four? One dimension, or two? It’s sort of…like…in between…?
Golda says: Although digitidiness explains a lot of what we see in our data, it doesn’t explain it all. I believe that desktop tidiness and mobile tidiness are different, if related, tendencies. For example, when we use mobile phones, we’re typically on-the-go and have less time. If we knew more about the people in our sample, we might see that these discrepancies in the organization of apps and tabs actually relate to other aspects of their lives. So, I say there are two dimensions.
Sidney says: Digitidiness is the only real factor here, but people may not always be consistent in these particular behaviors. Also some people are only sort-of-tidy, and apply this tidiness unevenly and randomly. These two-kinds of people choices don’t leave room for shades of gray, so that’s what we’re seeing in the mixed categories where people are tidy in one environment and not in another. But ultimately there is really just one dimension here.
What do you think?
(a) If the categories for each question are A, B, and C, we can get AA, AB, AC, BA, BB, … etc. We multiply the number of categories as many times as we have questions. So 3*3 = 9. (b) This time we have three questions, and for each one we have two options, so there are 2*2*2=8 possible combinations.↩︎